Module 4: Finding differentially expressed genes from RNAseq data

In this exercise, we will use edgeR to call differentially-expressed genes. For the example we will use an RNAseq dataset from a treatment-vehicle design.

If you haven’t already done so, install the airway dataset:

# BiocManager::install("airway")

These data are from the paper:

Himes BE, Jiang X, Wagner P, Hu R, Wang Q, Klanderman B, Whitaker RM, Duan Q, Lasky-Su J, Nikolos C, Jester W, Johnson M, Panettieri R Jr, Tantisira KG, Weiss ST, Lu Q. “RNA-Seq Transcriptome Profiling Identifies CRISPLD2 as a Glucocorticoid Responsive Gene that Modulates Cytokine Function in Airway Smooth Muscle Cells.” PLoS One. 2014 Jun 13;9(6):e99625. PMID: 24926665.

From the abstract of the original paper: “Using RNA-Seq, a high-throughput sequencing method, we characterized transcriptomic changes in four primary human ASM cell lines that were treated with dexamethasone - a potent synthetic glucocorticoid (1 micromolar for 18 hours).”

Let’s load the data

suppressMessages(library(airway))
data(airway)

These data happen to be in a Bioconductor-specific format, so we use the special functions, assay() and colData() to get the expression data and sample information.

xpr <- assay(airway)
samples <- colData(airway)

Questions:

  • How many samples are in this experiment?
  • How many genes were measured?
  • How many treatment groups are there (dex column)?

Let’s created a DGEList object (DGE stands for “Differential Gene Expression”). This object is what we will use for our differential expression analysis.

Note: Make phenotype of interest categorical. In R that means converting to a factor type with categorical levels. You can think of levels as ordinal representations (e.g., first level = 1, second = 2, etc., )

If levels= are not set, the default uses alphabetical order. We recommend explicitly setting levels so that there are no assumptions.

Load the edgeR package:

suppressMessages(library(edgeR))

Let’s create a DGEList object for the differential expression analysis. Note that group must be a categorical variable (use factor() to convert it to one):

group <- factor(samples$dex)
dge <- DGEList(
    counts = xpr,
    group = group
    )

Remove low-count genes: To filter low count genes, we’re going to use a normalized count measure called cpm (counts per million). We are going to keep genes with 100 or greater counts per million for at least two samples:

head(dge$counts)
##                 SRR1039508
## ENSG00000000003        679
## ENSG00000000005          0
## ENSG00000000419        467
## ENSG00000000457        260
## ENSG00000000460         60
## ENSG00000000938          0
##                 SRR1039509
## ENSG00000000003        448
## ENSG00000000005          0
## ENSG00000000419        515
## ENSG00000000457        211
## ENSG00000000460         55
## ENSG00000000938          0
##                 SRR1039512
## ENSG00000000003        873
## ENSG00000000005          0
## ENSG00000000419        621
## ENSG00000000457        263
## ENSG00000000460         40
## ENSG00000000938          2
##                 SRR1039513
## ENSG00000000003        408
## ENSG00000000005          0
## ENSG00000000419        365
## ENSG00000000457        164
## ENSG00000000460         35
## ENSG00000000938          0
##                 SRR1039516
## ENSG00000000003       1138
## ENSG00000000005          0
## ENSG00000000419        587
## ENSG00000000457        245
## ENSG00000000460         78
## ENSG00000000938          1
##                 SRR1039517
## ENSG00000000003       1047
## ENSG00000000005          0
## ENSG00000000419        799
## ENSG00000000457        331
## ENSG00000000460         63
## ENSG00000000938          0
##                 SRR1039520
## ENSG00000000003        770
## ENSG00000000005          0
## ENSG00000000419        417
## ENSG00000000457        233
## ENSG00000000460         76
## ENSG00000000938          0
##                 SRR1039521
## ENSG00000000003        572
## ENSG00000000005          0
## ENSG00000000419        508
## ENSG00000000457        229
## ENSG00000000460         60
## ENSG00000000938          0

Look at counts per million using cpm:

cpm(dge)[1:5,1:5]
##                 SRR1039508
## ENSG00000000003  32.900521
## ENSG00000000005   0.000000
## ENSG00000000419  22.628193
## ENSG00000000457  12.598138
## ENSG00000000460   2.907263
##                 SRR1039509
## ENSG00000000003  23.817776
## ENSG00000000005   0.000000
## ENSG00000000419  27.379809
## ENSG00000000457  11.217747
## ENSG00000000460   2.924057
##                 SRR1039512
## ENSG00000000003  34.439705
## ENSG00000000005   0.000000
## ENSG00000000419  24.498347
## ENSG00000000457  10.375306
## ENSG00000000460   1.577993
##                 SRR1039513
## ENSG00000000003  26.906868
## ENSG00000000005   0.000000
## ENSG00000000419  24.071095
## ENSG00000000457  10.815506
## ENSG00000000460   2.308187
##                 SRR1039516
## ENSG00000000003  46.546998
## ENSG00000000005   0.000000
## ENSG00000000419  24.009743
## ENSG00000000457  10.021102
## ENSG00000000460   3.190392

This next line is a bit complex so let’s unpack it:

  • We are using cpm(dge)>100 as a logical test (“which genes have cpm > 100?”).
  • For each gene, we want that test to be true for at least two samples. For this we use rowSums() to add up how many samples meet that criteria.
dim(dge) #before 
## [1] 63677     8
# keep genes which have cpm>100 in 2 or more samples
tokeep <- rowSums(cpm(dge)>100) >= 2 

# now filter for these
dge <- dge[tokeep,keep.lib.sizes = FALSE]

# how many genes do we have left?
dim(dge) #after
## [1] 2086    8

Normalize the data:

dge <- calcNormFactors(dge)

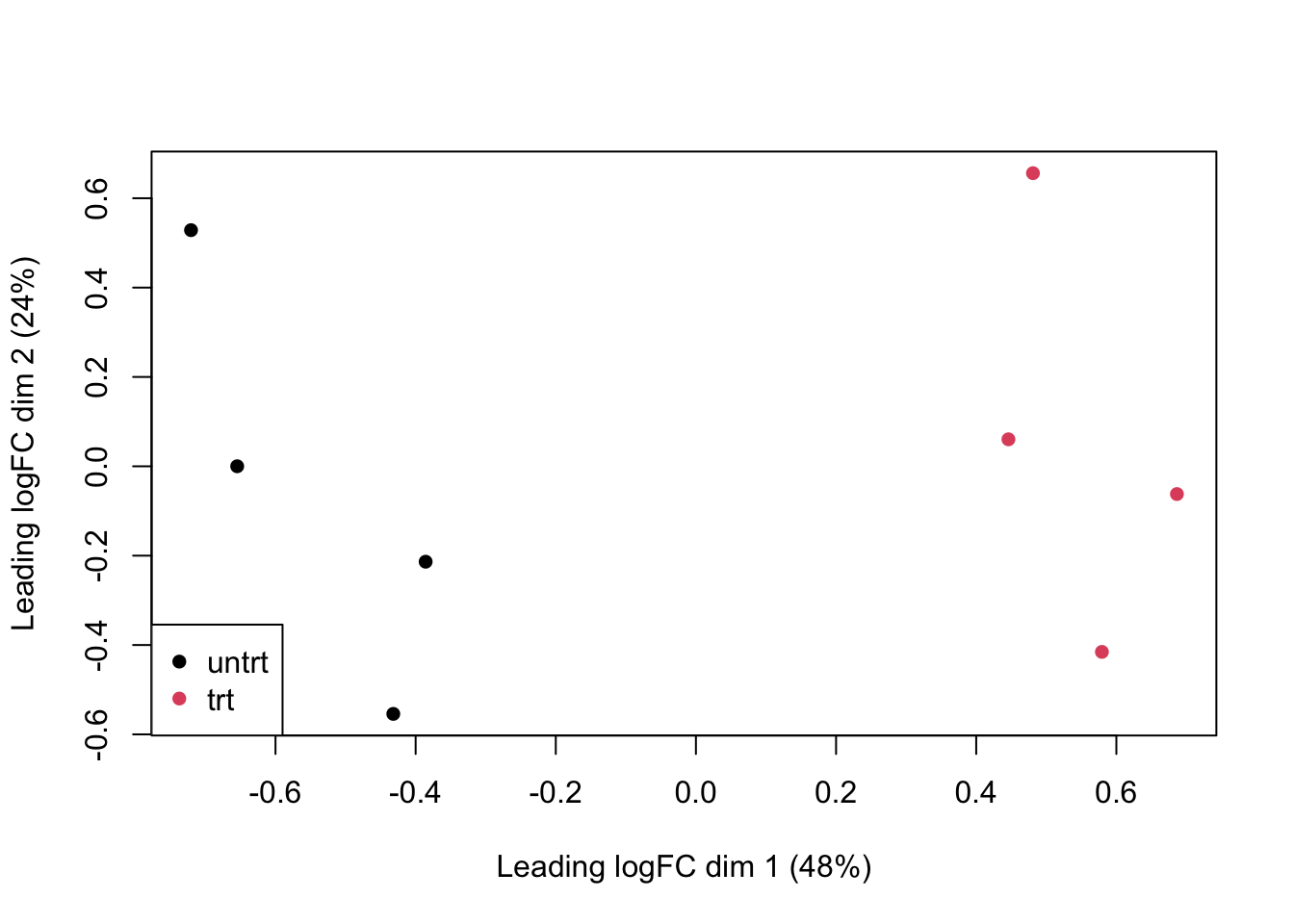
Visualize the data:

plotMDS(
    dge, 
    col=as.numeric(dge$samples$group), 
    pch=16
)
legend(
    "bottomleft", 
    as.character(unique(dge$samples$group)),
    col=c(1,2), pch=16
    )

Let’s create a model design to identify genes with a group effect:

group <- dge$samples$group
mod <- model.matrix(~group)

Estimate variation (“dispersion”) for each gene:

dge <- estimateDisp(dge, mod)

Call differentially expressed genes.

Here we:

  • fit a model for each gene, using glmFit
  • we have built in an estimate of gene-wise dispersion to better identify treatment effect (or “contrast”)
  • for each gene, we run a likelihood ratio test which compares which model fits the data better: a null model (treatment effect = 0) or a full model (treatment effect is non-zero)

Note that coef=2 fetches the effects for the treatment effect; coef=1 would fetch effects of the intercept term.
  

fit <- glmFit(dge,mod)
diffEx <- glmLRT(fit, coef = 2) # get coefficients for group term

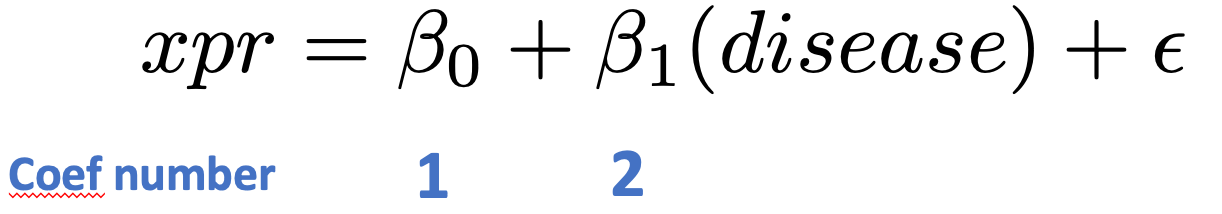
Look at the top 10 differentially expressed genes:

tt <- topTags(diffEx, n=10)
tt
## Coefficient:  groupuntrt 
##                     logFC
## ENSG00000152583 -4.512108
## ENSG00000178695  2.592010
## ENSG00000120129 -2.857535
## ENSG00000189221 -3.213455
## ENSG00000125148 -2.110664
## ENSG00000162614 -1.938280
## ENSG00000101347 -3.764745
## ENSG00000096060 -3.849662
## ENSG00000134686 -1.294763
## ENSG00000166741 -2.072008
##                   logCPM
## ENSG00000152583 5.950547
## ENSG00000178695 7.433587
## ENSG00000120129 7.727638
## ENSG00000189221 7.183776
## ENSG00000125148 7.835949
## ENSG00000162614 8.397283
## ENSG00000101347 9.620058
## ENSG00000096060 7.313033
## ENSG00000134686 7.426574
## ENSG00000166741 8.859215
##                       LR
## ENSG00000152583 190.5712
## ENSG00000178695 171.7187
## ENSG00000120129 167.2022
## ENSG00000189221 162.3746
## ENSG00000125148 156.1280
## ENSG00000162614 135.2052
## ENSG00000101347 128.9686
## ENSG00000096060 123.8841
## ENSG00000134686 121.0663
## ENSG00000166741 114.0478
##                       PValue
## ENSG00000152583 2.385925e-43
## ENSG00000178695 3.117449e-39
## ENSG00000120129 3.021823e-38
## ENSG00000189221 3.426477e-37
## ENSG00000125148 7.937896e-36
## ENSG00000162614 2.977497e-31
## ENSG00000101347 6.889897e-30
## ENSG00000096060 8.930961e-29
## ENSG00000134686 3.695702e-28
## ENSG00000166741 1.272045e-26
##                          FDR
## ENSG00000152583 4.977039e-40
## ENSG00000178695 3.251499e-36
## ENSG00000120129 2.101174e-35
## ENSG00000189221 1.786908e-34
## ENSG00000125148 3.311690e-33
## ENSG00000162614 1.035176e-28
## ENSG00000101347 2.053189e-27
## ENSG00000096060 2.328748e-26
## ENSG00000134686 8.565816e-26
## ENSG00000166741 2.653486e-24

For the next steps we’re going to need stats on all the genes we’ve tested. So let’s get those:

tt <- as.data.frame(
    topTags(diffEx, n=nrow(dge)
    )
)

A QQplot directly compares the pvalues from our statistical tests to the expected values from a random uniform distribution (p-value selected at random).

A deviation from the x=y line (diagonal) towards the top indicates an enrichment of signal.

qqplot(
    tt$PValue, 
    runif(nrow(tt)), # randomly sample from uniform distribution
    xlab="p-values from real data",
    ylab="Randomly-sampled values from Uniform distribution",
    pch=16,cex=0.5
)

# x=y line as reference
abline(0,1,col="red")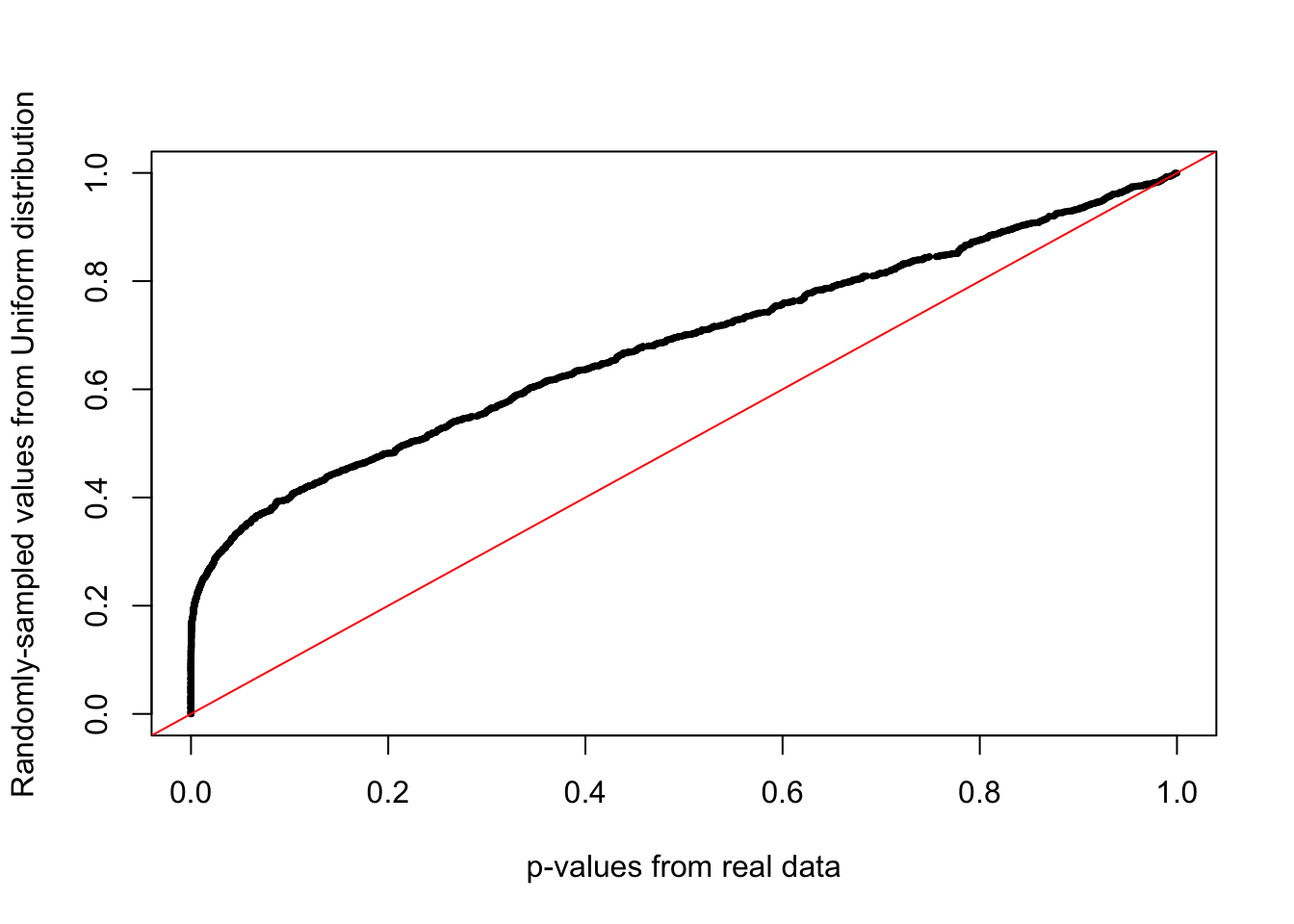

Now let’s call differentially expressed genes using the decideTestDGE() function and use summary() to see how many genes are upregulated (value +1), downregulated (value -1) and not called as changed (value 0)

diffEx2 <- decideTestsDGE(diffEx, 
    adjust.method="BH", 
    p.value=0.05
)
summary(diffEx2)
##        groupuntrt
## Down          317
## NotSig       1553
## Up            216

Volcano plot (R base graphics)

A volcano plot can help visualize effect magnitude - log2 fold-change or log2FC in the table ` against the corresponding p-value. Here we create a volcano plot, and colour-code upregulated genes in red, and downregulated genes in blue.

Let’s merge the data from tt and diffEx2 (which has the up-/down-regulated status):

# needed to use merge function
diffEx2 <- as.data.frame(diffEx2) 
# give column more intuitive name
colnames(diffEx2)[1] <- "gene_status"

# add the common "gene" column to merge the two tables
diffEx2$gene <- rownames(diffEx2)
tt$gene <- rownames(tt)

mega <- merge(x = tt, y = diffEx2, by="gene")

Now we create a vector of colours, so that our upregulated genes are in red, downregulated genes are in blue, and not-significant genes are in black:

cols <- rep("black",nrow(tt))
cols[which(mega$gene_status > 0)] <- "red" # upregulated
cols[which(mega$gene_status < 0)] <- "blue" # downregulated
mega$cols <- cols

# volcano plot
plot(mega$logFC,
    -log10(mega$PValue),
    pch=16, 
    col=mega$cols,
    xlab="log(fold-change)",
    ylab="-log10(p-value)"
)
abline(v=0,lty=3)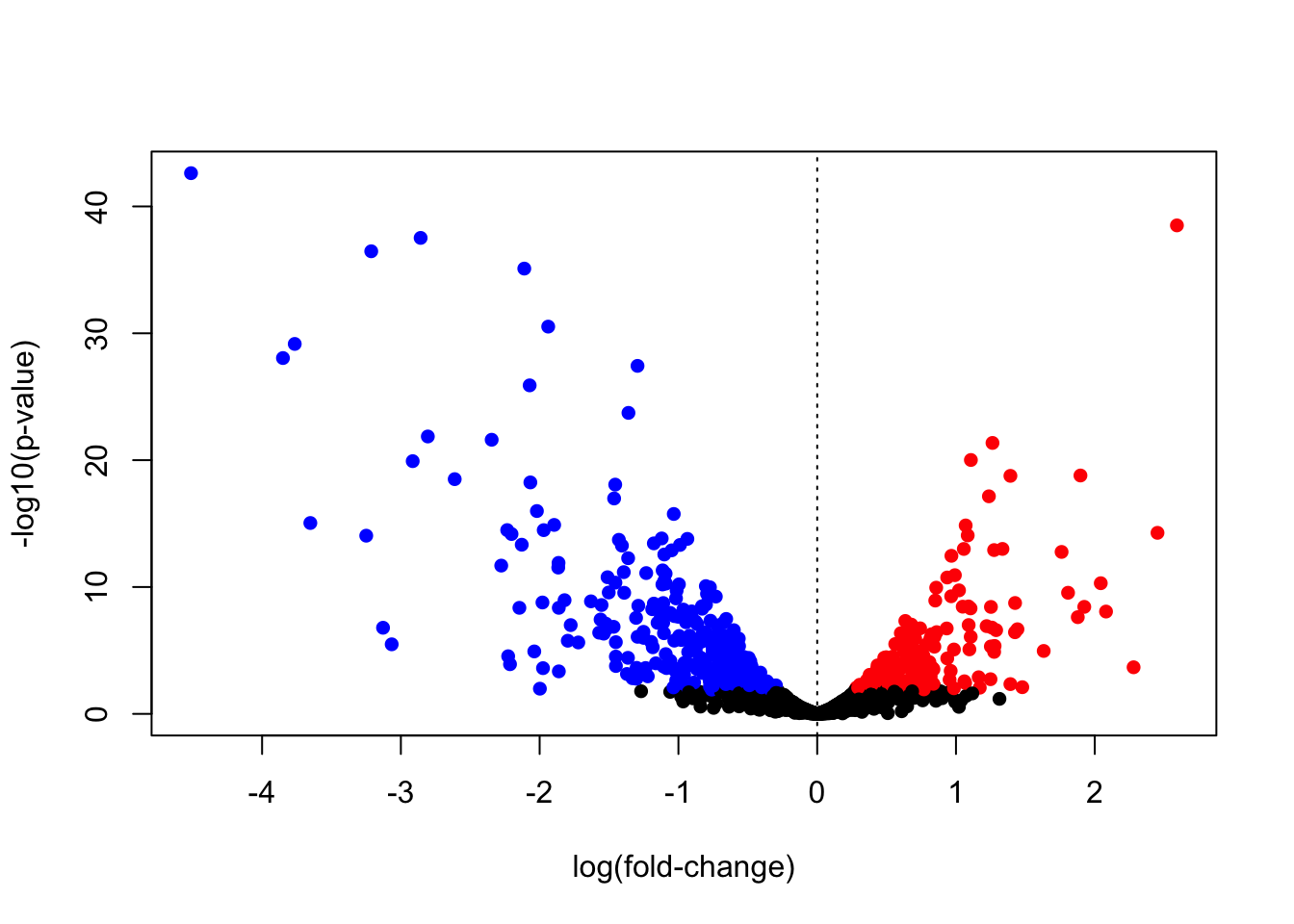

Volcano plot (ggplot2)

Let’s create a volcano plot using the ggplot2 library.

For this let’s add a NEW column indicating whether a gene is up-regulated, down-regulated, or n.s.

is_sig <- rep("n.s.", nrow(mega)) # default is ns
is_sig[which(mega$gene_status > 0)] <- "Upregulated"
is_sig[which(mega$gene_status < 0)] <- "Downregulated"

# use levels() to tell R how to order the categorical 
# variables. Downregulated = 1, n.s.=2, and Upregulated=3. 
# By default, R orders categorical variables alphabetically,
# which may not make sense!
mega$is_sig <- factor(is_sig, 
    levels = c("Downregulated","n.s.","Upregulated"))

Now let’s create a volcano plot, colouring the dots by significance status.

We will use scale_color_manual() from the ggplot2 package to add a custom colour scheme.

p1 <- ggplot(mega, 
    aes(x = logFC, y = -log10(FDR))) + # -log10 conversion  
    geom_point(aes(color=is_sig),size = 2/5) +  
    xlab(expression("log"[2]*"FC")) + 
    ylab(expression("-log"[10]*"FDR")) + 
    scale_color_manual(
        values = c("dodgerblue3", "gray50", "firebrick3")) 

p1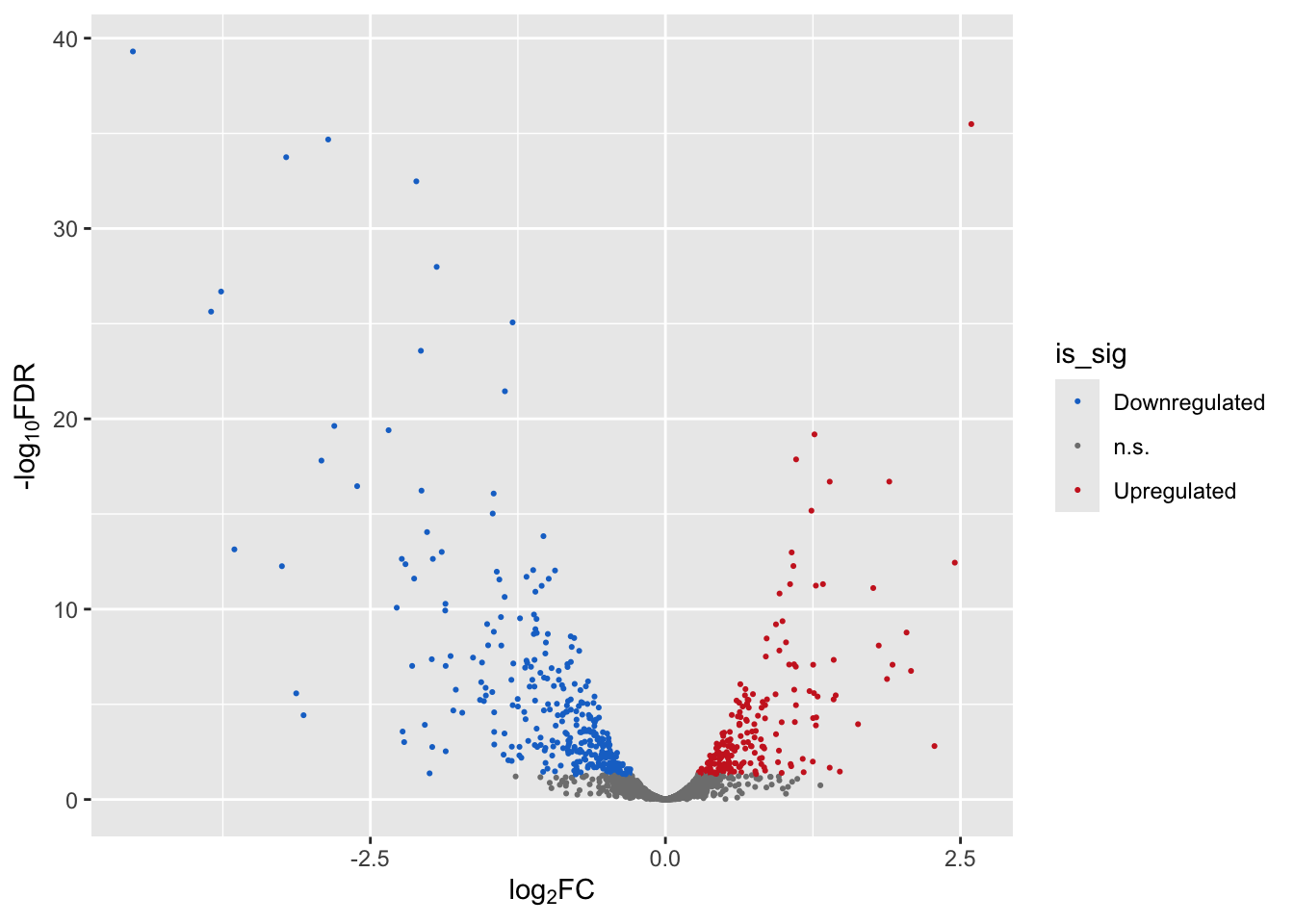

Finally we can write our differential expression results out to file:

write.table(mega,
    file="diffEx.results.txt",
    sep="\t",
    col=TRUE,
    row=TRUE,
    quote=FALSE
)

Bonus Exercise

  • Install the yeastRNASeq package from Bioconductor and library it into your environment
  • Import the geneLevelData using: data("geneLevelData")
  • Learn about this data and then put it through the same workflow we just did for the breast cancer:
  1. Create a new DGEList object with your gene counts
  2. Filter genes with CPM > 25 in at least two samples
  3. Normalize and plot your data
  4. Create a model matrix for analysis
  5. Fit your model
  6. How many significantly up-regulated genes are there at the 5% FDR level? How many significantly down-regulated genes? How many in total
  7. Create a volcano plot
  8. Bonus: Create a histogram of p-values. Is there a signal?

Is there anything about the data that might make you question the results?