Module 3: Generalized Linear Models

In this module we’re going to cover:

• Reading data from files and evaluating missingness
• Creating publication-quality plots with ggplot2
• Fitting models with binary outcomes using generalized linear models

Essential R: Reading tables from files, merging, basic data exploration

For this we’re going to use two data files available in the course data directory.

Download these for use and put them in your R working directory.

• tomerge1.csv : comma-separated values
• tomerge2.txt : space-delimited values

Use read.delim() to read in tables. Note the use of the sep= parameter to indicate what the column separator is:

x1 <- read.delim("AUR2024_data/tomerge1.csv",sep=",")
head(x1)

##   Sample_ID Exposure
## 1         A        0
## 2         B        0
## 3         C        0
## 4         D        0
## 5         E        1
## 6         F        1
##   Biomarker_value
## 1              35
## 2              22
## 3              91
## 4               3
## 5              56
## 6              37

x2 <- read.delim("AUR2024_data/tomerge2.txt",sep=" ")
head(x2)

##   sampleID Exposure_level
## 1        A     0.65405517
## 2        B     0.67202852
## 3        C     0.88646372
## 4        D     0.28433256
## 5        E     0.04166839
## 6        F     0.45263534
##   Biomarker2_detected
## 1                   1
## 2                   0
## 3                   1
## 4                   0
## 5                   0
## 6                   1

Use merge() to combine the two tables by sample ID. Note the use of by.x and by.y to tell merge() which columns are equivalent:

x_merge <- merge(x1, x2, by.x = "Sample_ID", by.y = "sampleID")
head(x_merge)

##   Sample_ID Exposure
## 1         A        0
## 2         B        0
## 3         C        0
## 4         D        0
## 5         E        1
## 6         F        1
##   Biomarker_value
## 1              35
## 2              22
## 3              91
## 4               3
## 5              56
## 6              37
##   Exposure_level
## 1     0.65405517
## 2     0.67202852
## 3     0.88646372
## 4     0.28433256
## 5     0.04166839
## 6     0.45263534
##   Biomarker2_detected
## 1                   1
## 2                   0
## 3                   1
## 4                   0
## 5                   0
## 6                   1

We’re going to use a popular dataset for data analysis, pertaining to survival of passengers aboard the Titanic.

Download the dataset here and copy it into your working directory.

Let’s read in the data from a file:

dat <- read.delim(
    "AUR2024_data/titanic.csv",
    sep="," # indicate the column separator
    ) 

Examine the columns:

head(dat)

##   PassengerId Survived Pclass
## 1           1        0      3
## 2           2        1      1
## 3           3        1      3
## 4           4        1      1
## 5           5        0      3
## 6           6        0      3
##                                                  Name
## 1                             Braund, Mr. Owen Harris
## 2 Cumings, Mrs. John Bradley (Florence Briggs Thayer)
## 3                              Heikkinen, Miss. Laina
## 4        Futrelle, Mrs. Jacques Heath (Lily May Peel)
## 5                            Allen, Mr. William Henry
## 6                                    Moran, Mr. James
##      Sex Age SibSp Parch
## 1   male  22     1     0
## 2 female  38     1     0
## 3 female  26     0     0
## 4 female  35     1     0
## 5   male  35     0     0
## 6   male  NA     0     0
##             Ticket    Fare
## 1        A/5 21171  7.2500
## 2         PC 17599 71.2833
## 3 STON/O2. 3101282  7.9250
## 4           113803 53.1000
## 5           373450  8.0500
## 6           330877  8.4583
##   Cabin Embarked
## 1              S
## 2   C85        C
## 3              S
## 4  C123        S
## 5              S
## 6              Q

Some of the columns are categorical, use table() to look at the tallies: Examine the columns:

table(dat$Survived)

## 
##   0   1 
## 549 342

table(dat$Pclass)

## 
##   1   2   3 
## 216 184 491

Use summary() to look at continuous-valued data:

summary(dat$Age)

##    Min. 1st Qu.  Median 
##    0.42   20.12   28.00 
##    Mean 3rd Qu.    Max. 
##   29.70   38.00   80.00 
##    NA's 
##     177

Notice that there are 177 NA (missing) values for age. Let’s visualize the missing data more systematically.

Explore missing data

For this let’s use a little script that converts a table into black and white squares to visualize missing data. For this, install the plotrix package

if (!requireNamespace("plotrix", quietly = TRUE)) install.packages("plotrix")

suppressMessages(library(plotrix))

#' show data missingness as a chequered matrix
#' 
#' @param x (matrix) data matrix.
#' @param outFile (char) path to file for printing graph
#' @param wd (numeric) width in inches
#' @param ht (numeric) height in inches
#' @return plots missingness matrix to file
#' @import plotrix
#' @export
plotMissMat <- function(x,xlab="columns",
        ylab="rows",border=NA) {
    
    x <- !is.na(x)
    class(x) <- "numeric"
    color2D.matplot(x,show.values=FALSE,axes=FALSE,
        cs1=c(1,0),cs2=c(1,0),cs3=c(1,0),border=border,
        cex=0.8,
        xlab=xlab,ylab=ylab)
}

Let’s look at the missingness in the Titanic dataset. Missing data is shown as a white cell, and non-missing data is shown in black.

plotMissMat(dat)

We can see a column with many missing values. This is probably the “age” data. Let’s count the number of missing values on a per-column level.

For this we combine is.na(), which returns a TRUE/FALSE value for NA values, and colSums() which adds up the TRUE values down the columns.

colSums(is.na(dat))

## PassengerId    Survived 
##           0           0 
##      Pclass        Name 
##           0           0 
##         Sex         Age 
##           0         177 
##       SibSp       Parch 
##           0           0 
##      Ticket        Fare 
##           0           0 
##       Cabin    Embarked 
##           0           0

This confirms that Age is the only column with missing data.

Now let’s explore the data using plots.

Essential R: Plots with ggplot2

ggplot2 is a popular plotting package that uses an additive paradigm to build plots.

Useful websites: * ggplot2 cheatsheet * The ggplot2 website is a wealth of reference information, so here we just touch on the basics to get you started.

Anytime you need to generate a specific kind of plot, the website will most likely have documentation for how to achieve it.

Let’s start by creating a scatterplot with two continuous variables. For this let’s load a dataset measuring statistics around quality of life in US states in the late 70’s:

state.x77 <- as.data.frame(state.x77)
head(state.x77)

##            Population Income
## Alabama          3615   3624
## Alaska            365   6315
## Arizona          2212   4530
## Arkansas         2110   3378
## California      21198   5114
## Colorado         2541   4884
##            Illiteracy
## Alabama           2.1
## Alaska            1.5
## Arizona           1.8
## Arkansas          1.9
## California        1.1
## Colorado          0.7
##            Life Exp Murder
## Alabama       69.05   15.1
## Alaska        69.31   11.3
## Arizona       70.55    7.8
## Arkansas      70.66   10.1
## California    71.71   10.3
## Colorado      72.06    6.8
##            HS Grad Frost
## Alabama       41.3    20
## Alaska        66.7   152
## Arizona       58.1    15
## Arkansas      39.9    65
## California    62.6    20
## Colorado      63.9   166
##              Area
## Alabama     50708
## Alaska     566432
## Arizona    113417
## Arkansas    51945
## California 156361
## Colorado   103766

Create a base plot using the ggplot function. Then “add” a scatterplot to it. Notice that the plot has been assigned to a variable named p.

This setup is standard for ggplot2 and allows multiple visualizations to be applied to the same base plot.

We use aes to tell ggplot what the x and y axes are, and later, if we want to colour-code by a particular column.

library(ggplot2)
p <- ggplot(state.x77, 
    aes(x = Illiteracy,y = Income)
    )

p <- p + geom_point() # scatter plot
p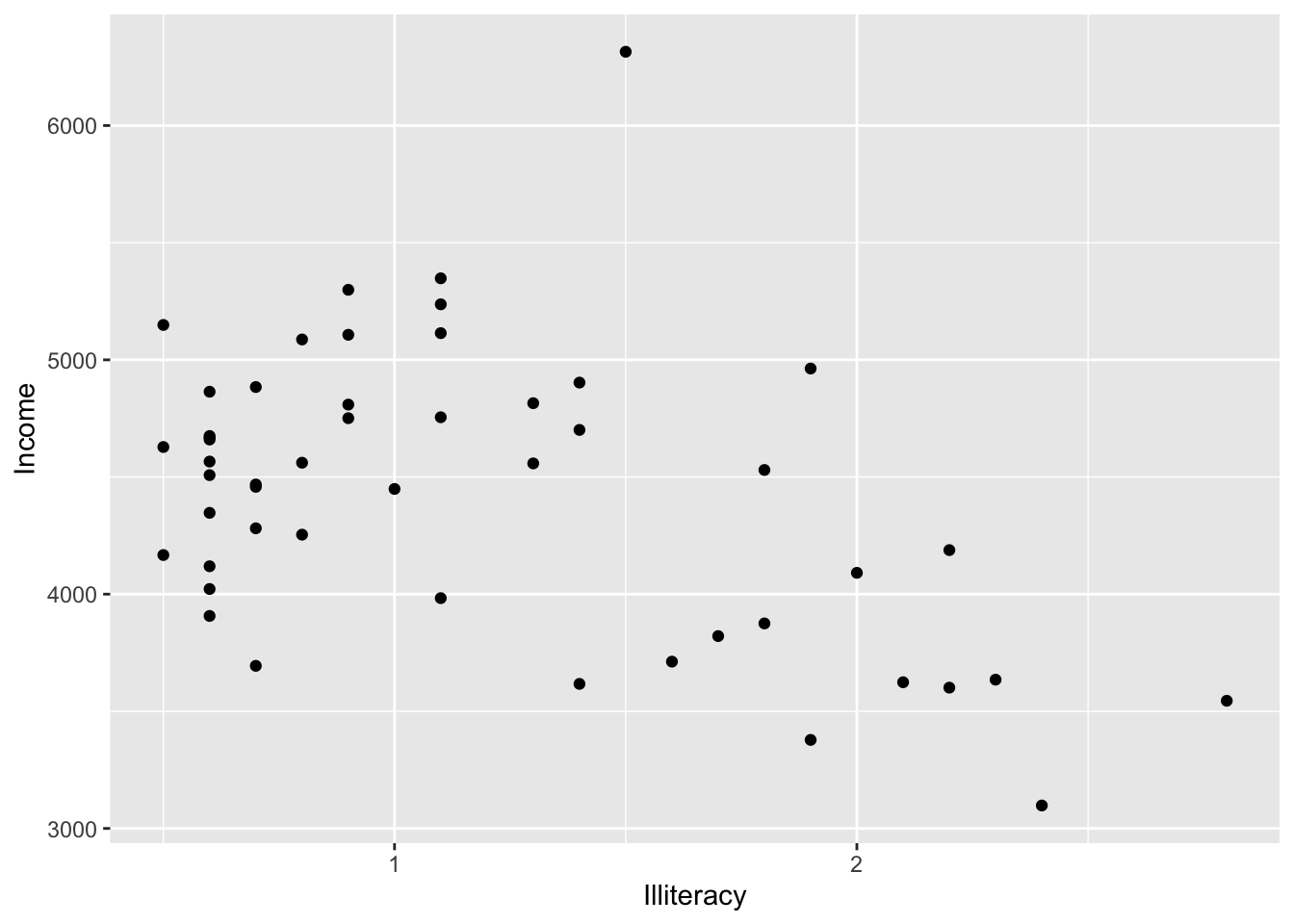

Now let’s add confidence intervals:

p + geom_smooth()

## `geom_smooth()` using method
## = 'loess' and formula = 'y ~
## x'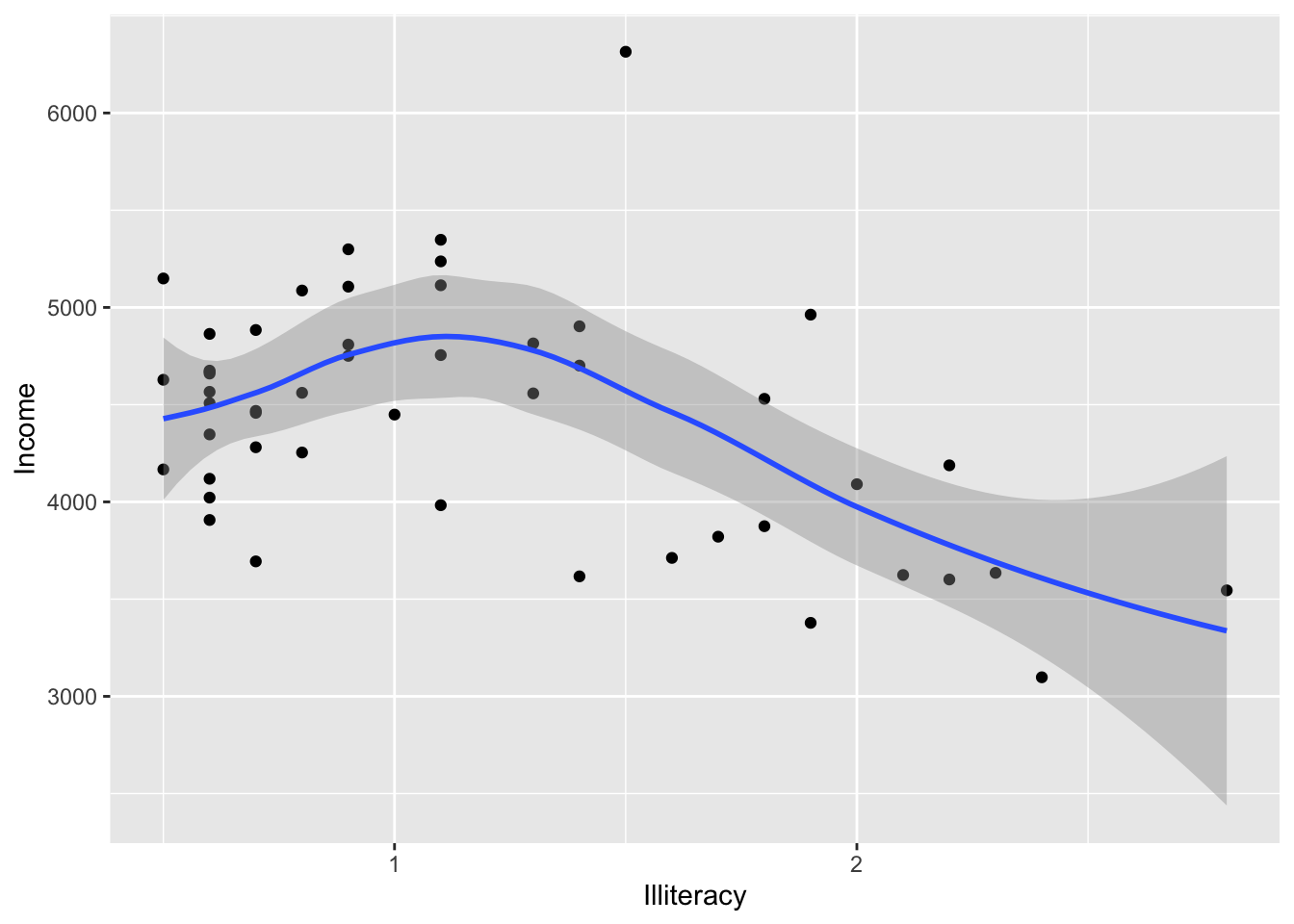

It looks like there is a negative relationship between illiteracy and income. We can confirm this by looking at correlation:

x <- state.x77$Illiteracy
y <- state.x77$Income
cor.test(x,y)

## 
##  Pearson's product-moment
##  correlation
## 
## data:  x and y
## t = -3.3668, df = 48,
## p-value = 0.001505
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.6378257 -0.1807128
## sample estimates:
##        cor 
## -0.4370752

cor.test(x,y)$p.value

## [1] 0.001505073

Let’s now examine categorical variables. In the titanic set, let’s look at the fare paid based on passenger class:

p <- ggplot(dat)
p + geom_boxplot(
    aes(x = factor(Pclass), # "factor()" makes a data column a categorical variable
        y = Fare))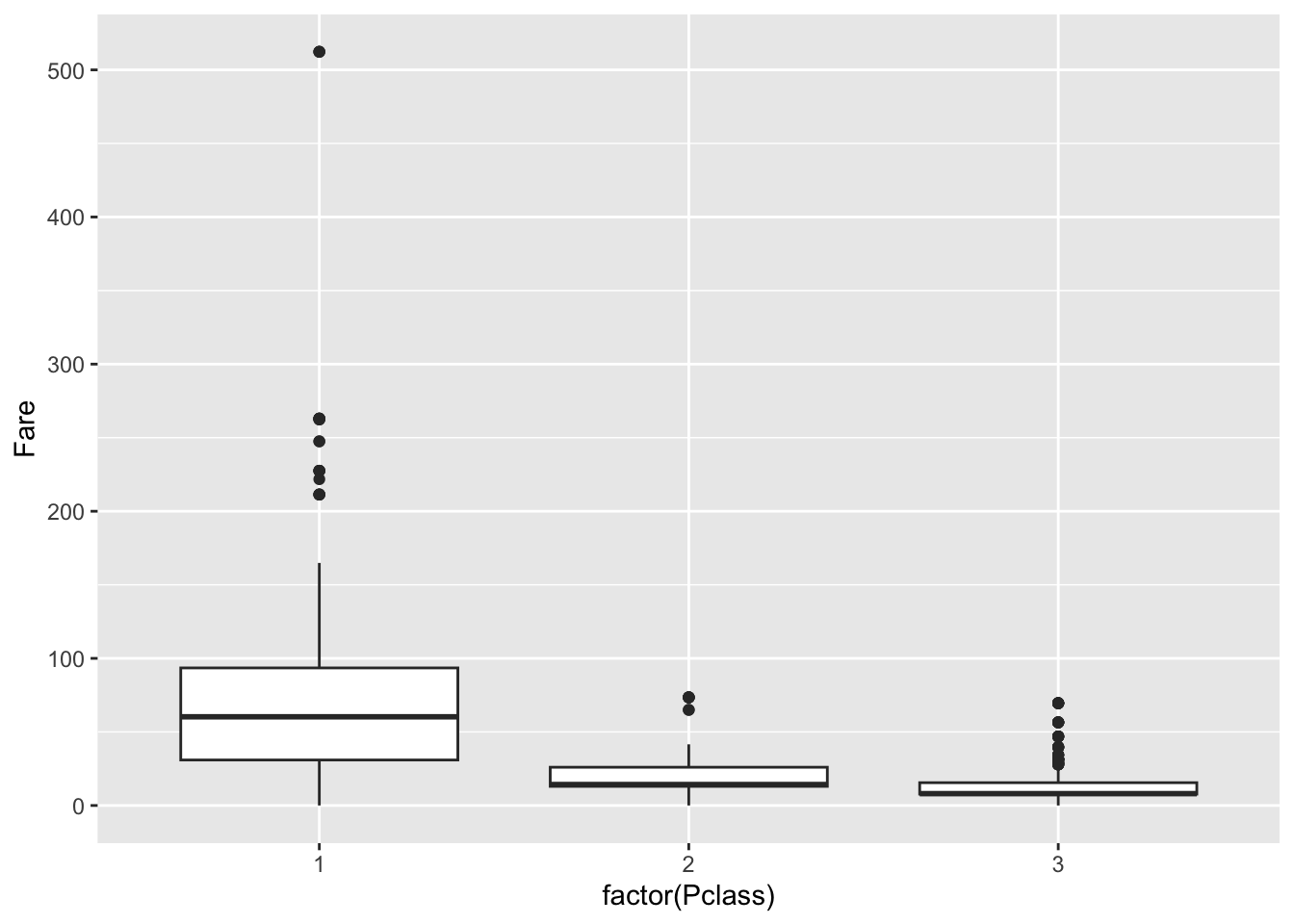

We can use barplots to examine counts and proportions. Let’s look at number of survivors, split by passenger class.

Here the fill command is used to to split each barplot by the category, “Survived”. So you can see number of passengers by “Pclass” split by survival.

p + geom_bar(
    aes(fill=factor(Survived), 
        x = Pclass)
)

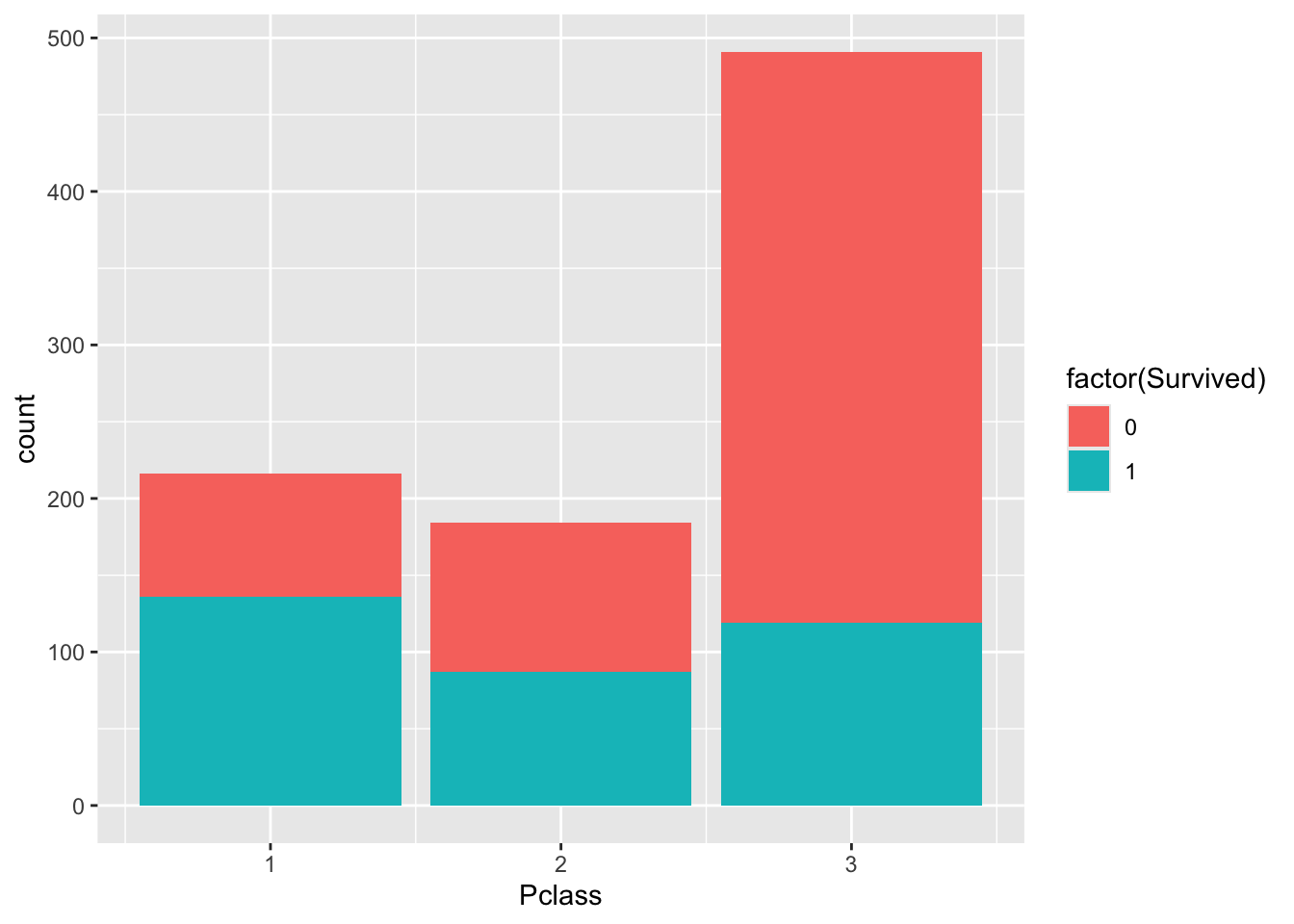
The plot above shows count data. Let’s convert this to proportions. We can see that the fraction of non-survivors in “Class 3” is high.

p + geom_bar(
    aes(fill=factor(Survived), x = Pclass),
    position = "fill"
)

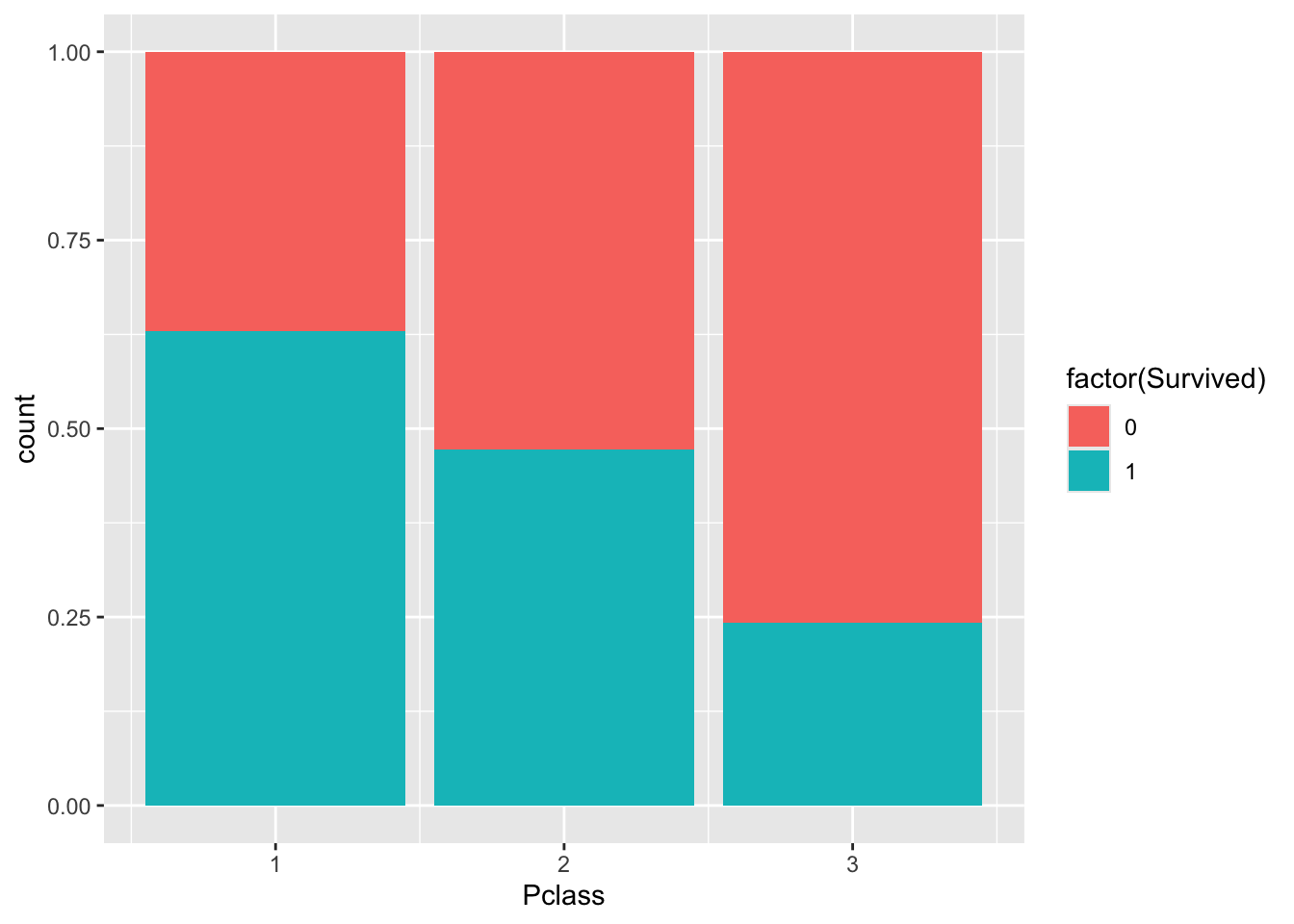
How about males versus females?

p + geom_bar(
    aes(fill=factor(Survived), x = Sex),
    position = "fill"
)

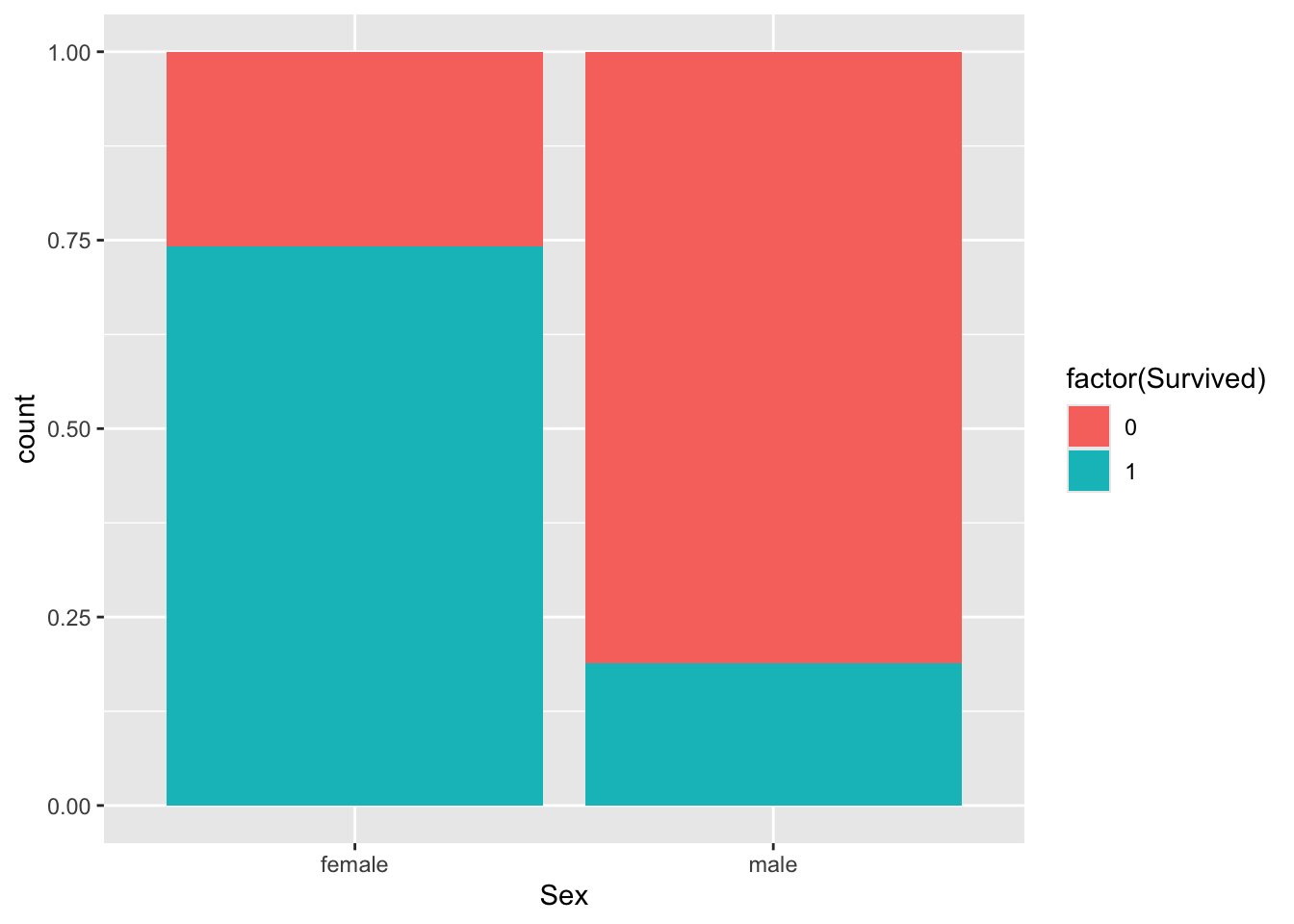
Exercise for later: Try other ggplot functions on these data or on a small data table of your project. (avoid using large genomics datasets, because those are going to be harder to interpret)

Fit binary response variable using glm() and logistic regression

Let’s fit a model to a binary outcome. For this we load a dataset that measures physiological variables in a cohort of Pima Indians.

library(mlbench)
data(PimaIndiansDiabetes2)
# type ?PimaIndiansDiabetes2 to learn more about the dataset.

dat <- PimaIndiansDiabetes2
head(dat)

##   pregnant glucose pressure
## 1        6     148       72
## 2        1      85       66
## 3        8     183       64
## 4        1      89       66
## 5        0     137       40
## 6        5     116       74
##   triceps insulin mass
## 1      35      NA 33.6
## 2      29      NA 26.6
## 3      NA      NA 23.3
## 4      23      94 28.1
## 5      35     168 43.1
## 6      NA      NA 25.6
##   pedigree age diabetes
## 1    0.627  50      pos
## 2    0.351  31      neg
## 3    0.672  32      pos
## 4    0.167  21      neg
## 5    2.288  33      pos
## 6    0.201  30      neg

Let’s look at the impact of blood glucose levels on diabetes diagnosis.

First let’s make a scatterplot. Could there be a relationship?

p <- ggplot(dat, aes(x = glucose, y = factor(diabetes)))
p + geom_point()

## Warning: Removed 5 rows containing
## missing values or values
## outside the scale range
## (`geom_point()`).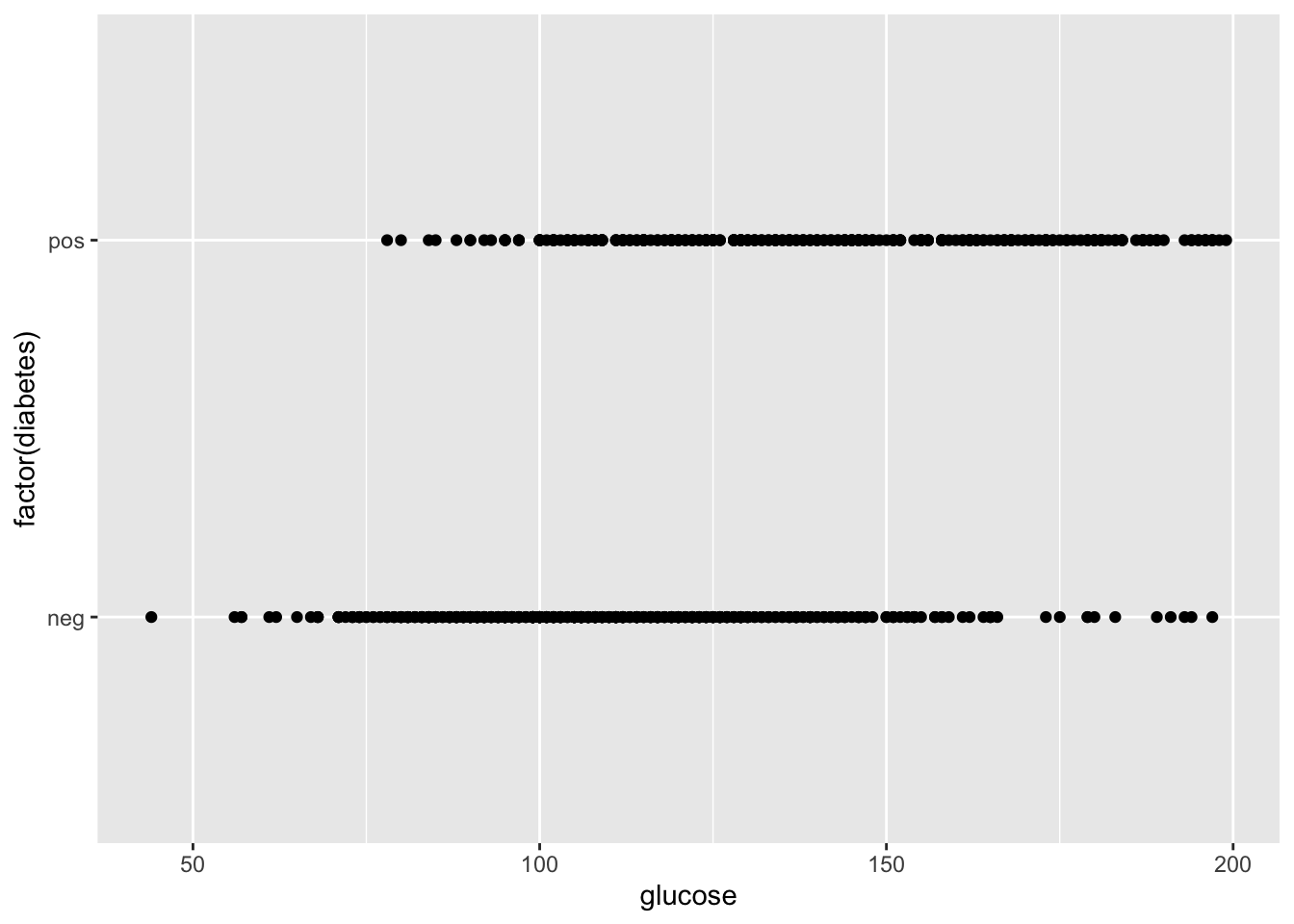

Could this be fit with a linear model?

Is there a continuous line that could reasonably fit the data?

p <- ggplot(dat, aes(x = glucose, y = factor(diabetes)))
p + geom_point() + geom_smooth()

## `geom_smooth()` using method
## = 'loess' and formula = 'y ~
## x'

## Warning: Removed 5 rows containing
## non-finite outside the scale
## range (`stat_smooth()`).

## Warning: Removed 5 rows containing
## missing values or values
## outside the scale range
## (`geom_point()`).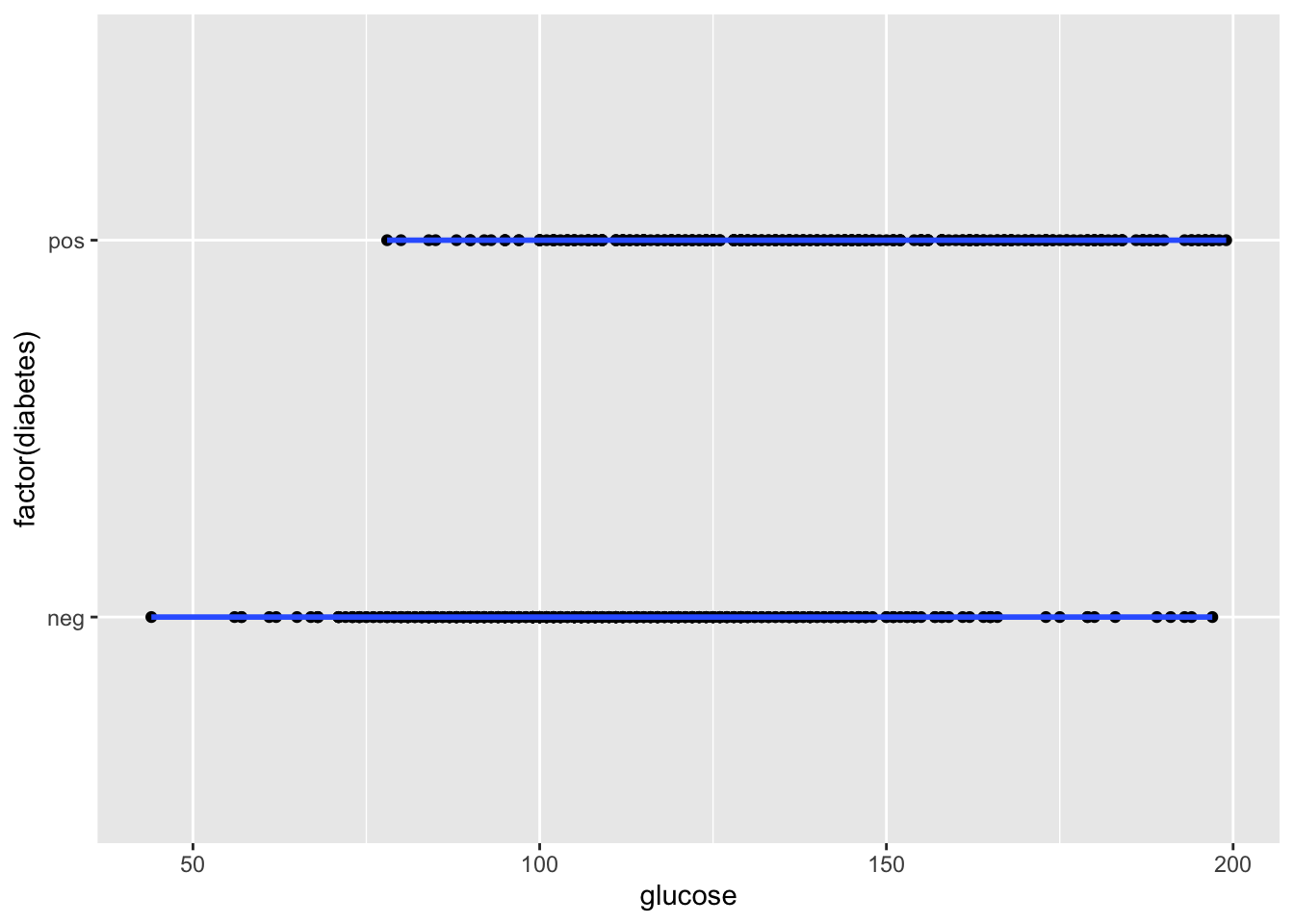

This is a situation where a logistic regression model would be an appropriate choice because of the binary outcome.

We’re going to use glm() to fit a model to these data:

mod <- glm(factor(diabetes)~glucose, 
    dat,
    family = "binomial" # set to model binary outcome
)
summary(mod)

## 
## Call:
## glm(formula = factor(diabetes) ~ glucose, family = "binomial", 
##     data = dat)
## 
## Coefficients:
##              Estimate
## (Intercept) -5.715088
## glucose      0.040634
##             Std. Error
## (Intercept)   0.438100
## glucose       0.003382
##             z value Pr(>|z|)
## (Intercept)  -13.04   <2e-16
## glucose       12.01   <2e-16
##                
## (Intercept) ***
## glucose     ***
## ---
## Signif. codes:  
##   0 '***' 0.001 '**' 0.01
##   '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 986.70  on 762  degrees of freedom
## Residual deviance: 786.56  on 761  degrees of freedom
##   (5 observations deleted due to missingness)
## AIC: 790.56
## 
## Number of Fisher Scoring iterations: 4

Which factors explain a diabetes diagnosis?

What if we include a couple other factors?

mod <- glm(factor(diabetes)~ glucose + pregnant + age + pressure + triceps,
    dat,
    family = "binomial")
summary(mod)

## 
## Call:
## glm(formula = factor(diabetes) ~ glucose + pregnant + age + pressure + 
##     triceps, family = "binomial", data = dat)
## 
## Coefficients:
##               Estimate
## (Intercept) -7.6685706
## glucose      0.0365926
## pregnant     0.0972493
## age          0.0249707
## pressure    -0.0009321
## triceps      0.0420045
##             Std. Error
## (Intercept)  0.8451262
## glucose      0.0041105
## pregnant     0.0417560
## age          0.0135945
## pressure     0.0099322
## triceps      0.0117044
##             z value Pr(>|z|)
## (Intercept)  -9.074  < 2e-16
## glucose       8.902  < 2e-16
## pregnant      2.329 0.019860
## age           1.837 0.066235
## pressure     -0.094 0.925230
## triceps       3.589 0.000332
##                
## (Intercept) ***
## glucose     ***
## pregnant    *  
## age         .  
## pressure       
## triceps     ***
## ---
## Signif. codes:  
##   0 '***' 0.001 '**' 0.01
##   '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 678.40  on 533  degrees of freedom
## Residual deviance: 494.38  on 528  degrees of freedom
##   (234 observations deleted due to missingness)
## AIC: 506.38
## 
## Number of Fisher Scoring iterations: 5

Note: This morning’s session only intends to introduce you to fitting non-linear models.

In practice you may need to do more work to test multiple models to ascertain best fits your data, using measures such as goodness-of-fit. You will also likely compute odds ratio (odds of increased Y per unit increase X), which is out of scope for the current tutorial.

We strongly recommend that you learn these topics before applying these methods to your own data.

Bonus Exercise

Now let’s apply the ideas above to a dataset for classifying a breast cell as being either benign or malignant.

data(BreastCancer)
bc <- BreastCancer
for (k in 2:10) # altered for current lab
    bc[,k] <- as.numeric(bc[,k]) 
head(bc)

##        Id Cl.thickness
## 1 1000025            5
## 2 1002945            5
## 3 1015425            3
## 4 1016277            6
## 5 1017023            4
## 6 1017122            8
##   Cell.size Cell.shape
## 1         1          1
## 2         4          4
## 3         1          1
## 4         8          8
## 5         1          1
## 6        10         10
##   Marg.adhesion Epith.c.size
## 1             1            2
## 2             5            7
## 3             1            2
## 4             1            3
## 5             3            2
## 6             8            7
##   Bare.nuclei Bl.cromatin
## 1           1           3
## 2          10           3
## 3           2           3
## 4           4           3
## 5           1           3
## 6          10           9
##   Normal.nucleoli Mitoses
## 1               1       1
## 2               2       1
## 3               1       1
## 4               7       1
## 5               1       1
## 6               7       1
##       Class
## 1    benign
## 2    benign
## 3    benign
## 4    benign
## 5    benign
## 6 malignant

Learn more about the dataset:

?BreastCancer

For your exercise, answer the following questions:

• Is there missing data?
• Which columns are
• Use plots to explore the relationship between explanatory variables.
• Fit a logistic model to identify which factors explain class (benign vs. malignant).