Module 1: Exploratory Data Analysis and Clustering
The goal of this lab is to examine correlation structure in a sample transcriptomic dataset using clustering.
Specifically, we will:
- Load and briefly explore transcriptomic measures from two mouse tissues
- Explore the correlation structure in the data using
pairs() - See the effect of running k-means and hierarchical clustering on the data
- Use
clValidto find out what cluster number best separates groups
We will explore missing data in detail in Module 3.
Load mouse data
For this exercise we are going to load a dataset built into the clValid package.
This dataset measures 147 genes and expressed sequence tags in two developing mouse lineages: the neural crest cells and mesoderm-derived cells.
There are three samples per group.
Let’s load the data.
suppressMessages(library(clValid))
data(mouse)Use str() to see what types of data the columns have:
str(mouse)## 'data.frame': 147 obs. of 8 variables:
## $ ID : Factor w/ 147 levels "1415787_at","1415904_at",..: 111 88 93 74 138 103 46 114 112 24 ...
## $ M1 : num 4.71 3.87 2.88 5.33 5.37 ...
## $ M2 : num 4.53 4.05 3.38 5.5 4.55 ...
## $ M3 : num 4.33 3.47 3.24 5.63 5.7 ...
## $ NC1: num 5.57 5 3.88 6.8 6.41 ...
## $ NC2: num 6.92 5.06 4.46 6.54 6.31 ...
## $ NC3: num 7.35 5.18 4.85 6.62 6.2 ...
## $ FC : Factor w/ 9 levels "ECM/Receptors",..: 3 8 6 6 1 3 1 6 5 6 ...Another command is head():
head(mouse)## ID M1 M2 M3 NC1 NC2 NC3
## 1 1448995_at 4.706812 4.528291 4.325836 5.568435 6.915079 7.353144
## 2 1436392_s_at 3.867962 4.052354 3.474651 4.995836 5.056199 5.183585
## 3 1437434_a_at 2.875112 3.379619 3.239800 3.877053 4.459629 4.850978
## 4 1428922_at 5.326943 5.498930 5.629814 6.795194 6.535522 6.622577
## 5 1452671_s_at 5.370125 4.546810 5.704810 6.407555 6.310487 6.195847
## 6 1448147_at 3.471347 4.129992 3.964431 4.474737 5.185631 5.177967
## FC
## 1 Growth/Differentiation
## 2 Transcription factor
## 3 Miscellaneous
## 4 Miscellaneous
## 5 ECM/Receptors
## 6 Growth/DifferentiationSummary provides useful information about the distribution of variables. Note that FC has categorical variables:
summary(mouse)## ID M1 M2 M3 NC1
## 1415787_at: 1 Min. :2.352 Min. :2.139 Min. :2.500 Min. :2.100
## 1415904_at: 1 1st Qu.:4.188 1st Qu.:4.151 1st Qu.:4.207 1st Qu.:4.174
## 1415993_at: 1 Median :4.994 Median :5.043 Median :5.054 Median :4.996
## 1416164_at: 1 Mean :5.166 Mean :5.140 Mean :5.231 Mean :5.120
## 1416181_at: 1 3rd Qu.:6.147 3rd Qu.:6.015 3rd Qu.:6.129 3rd Qu.:5.860
## 1416221_at: 1 Max. :9.282 Max. :9.273 Max. :9.228 Max. :8.905
## (Other) :141
## NC2 NC3 FC
## Min. :1.996 Min. :2.125 EST :31
## 1st Qu.:4.136 1st Qu.:4.293 Transcription factor :28
## Median :5.056 Median :4.974 Miscellaneous :25
## Mean :5.134 Mean :5.118 ECM/Receptors :16
## 3rd Qu.:5.920 3rd Qu.:5.826 Growth/Differentiation:16
## Max. :8.954 Max. :9.251 Unknown :10
## (Other) :21What are the values in FC?
table(mouse$FC)##
## ECM/Receptors EST Growth/Differentiation
## 16 31 16
## Kinases/Phosphatases Metabolism Miscellaneous
## 7 8 25
## Stress-induced Transcription factor Unknown
## 6 28 10Let’s use pairs() to look at pairwise scatterplots of the expression data in a single plot. We need to subset the columns with the expression data first:
mouse_exp = mouse[,c("M1","M2","M3","NC1","NC2","NC3")]
pairs(mouse_exp)
RColorBrewer for colour palettes
Visualization often requires assigning colours to categories of interest (e.g., two different tissue types, eight levels of doses).
RColorBrewer is a good package to pick a colour scheme for your project, as palettes are derived using colour science:
Let’s look at all the palettes available.
library(RColorBrewer)
display.brewer.all()
We’re going to use RColorBrewer to assign colours to our heatmap below.
Correlations, distances, and clustering
Let’s look at sample correlation matrix. This should be a square matrix, equal to the number of samples.
We have six samples, so the correlation matrix should be 6x6.
library(corrplot)
mouse_cor <- cor(mouse_exp)
dim(mouse_cor)## [1] 6 6round(mouse_cor,2)## M1 M2 M3 NC1 NC2 NC3
## M1 1.00 0.98 0.98 0.84 0.81 0.78
## M2 0.98 1.00 0.95 0.84 0.81 0.79
## M3 0.98 0.95 1.00 0.82 0.78 0.75
## NC1 0.84 0.84 0.82 1.00 0.97 0.95
## NC2 0.81 0.81 0.78 0.97 1.00 0.99
## NC3 0.78 0.79 0.75 0.95 0.99 1.00corrplot(mouse_cor, method="color")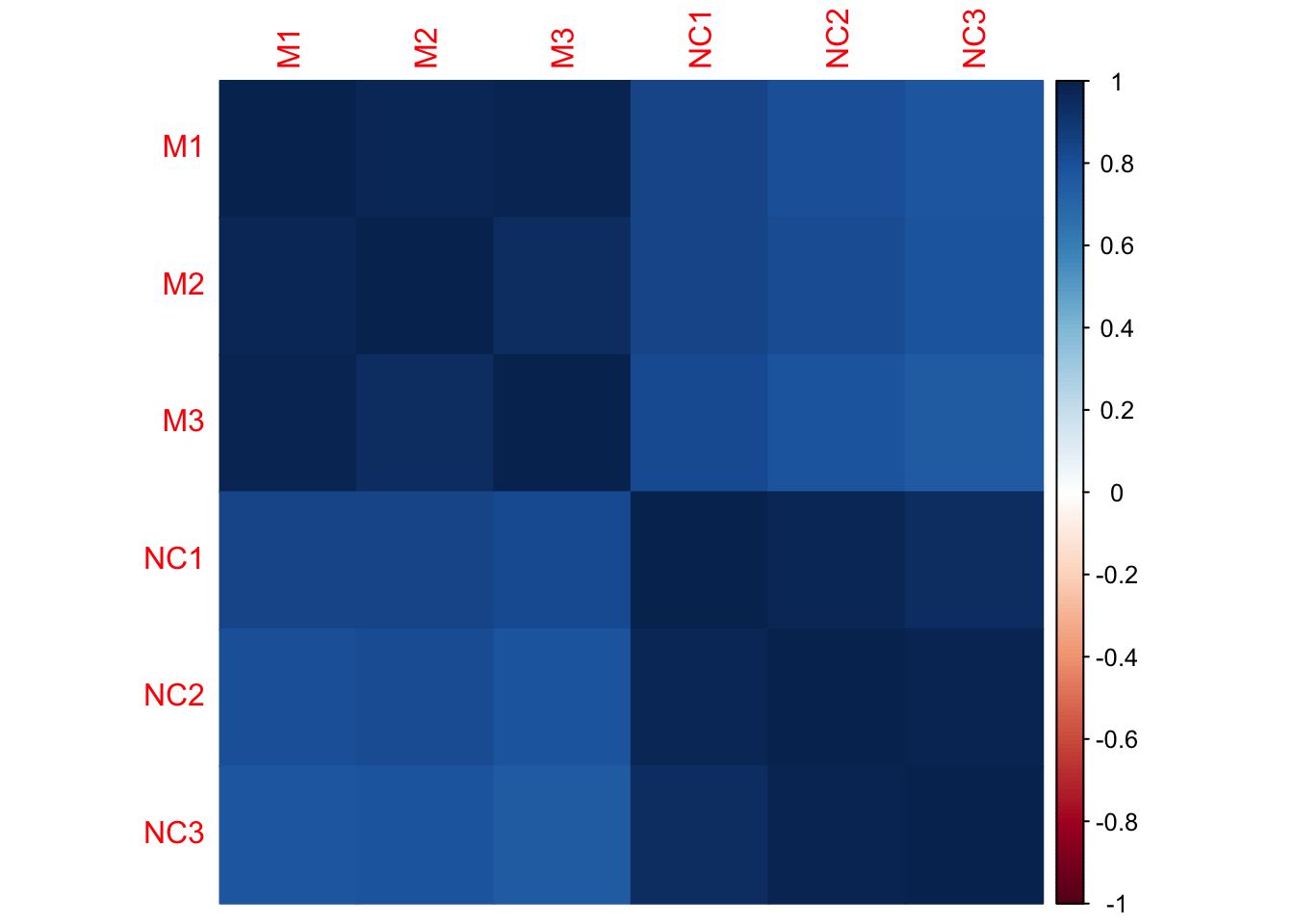
- Which samples appear to be best correlated with each other?
- Which samples don’t appear to be as well correlated with each other?
Hierarchical clustering
Hierarchical clustering requires distances between samples. Let’s use dist() to compute these distances, and hclust() to generate the hierarchical clustering object.
Different values for method can produce different results. In our experience complete or ward.D2 produce stable results.
d <- dist(log(mouse_exp))
h <- hclust(d,method="ward.D2")
plot(h)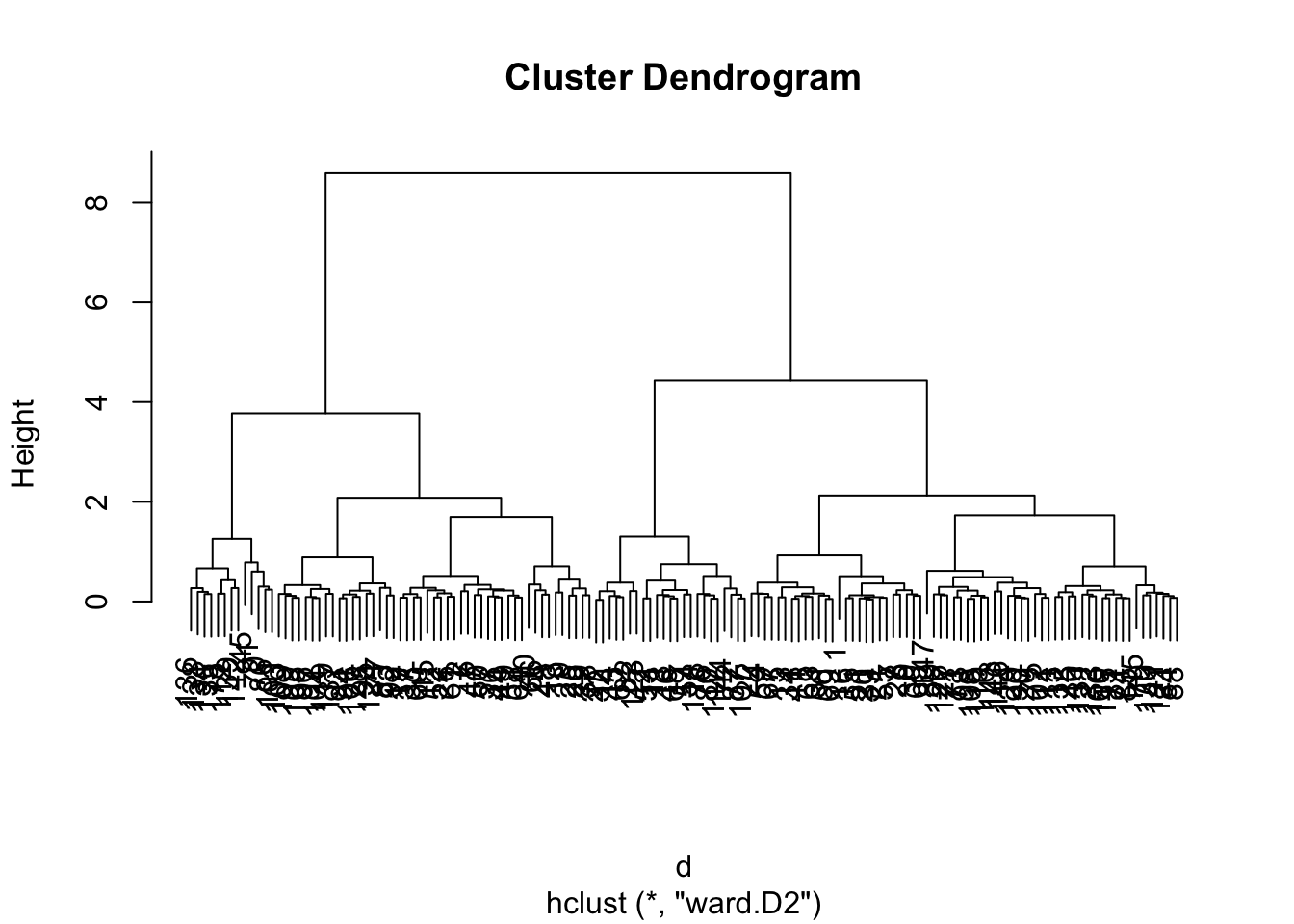
Can you guess how many clusters could best fit the data?
Now let’s add a heatmap to this dendrogram, so we can see the values of genes in each cluster. For this we will use the heatmap() function, which requires assigned cluster labels to each sample, and a dendrogram-generating function.
So let’s create these.
First we get cluster assignments by “cutting” the dendrogram for two clusters (something we expect from our experimental design). We use cutree() for this. Then assign colours based on cluster assignment.
h2 <- cutree(h, k = 2)
h2cols <- c("orangered","blue")[h2]Now define a hierarchical clustering function:
hclust_fun <- function(x){
f <- hclust(x, method = "ward.D2");
return(f)
}And finally supply the two to the heatmap() function:
heatmap(
as.matrix(mouse_exp),
col = brewer.pal("Blues",n=8),
hclustfun = hclust_fun,
RowSideColors = h2cols, # use colours from cutree call above
ColSideColors = c(
rep("darkgreen",3),
rep("deeppink2",3)
)
)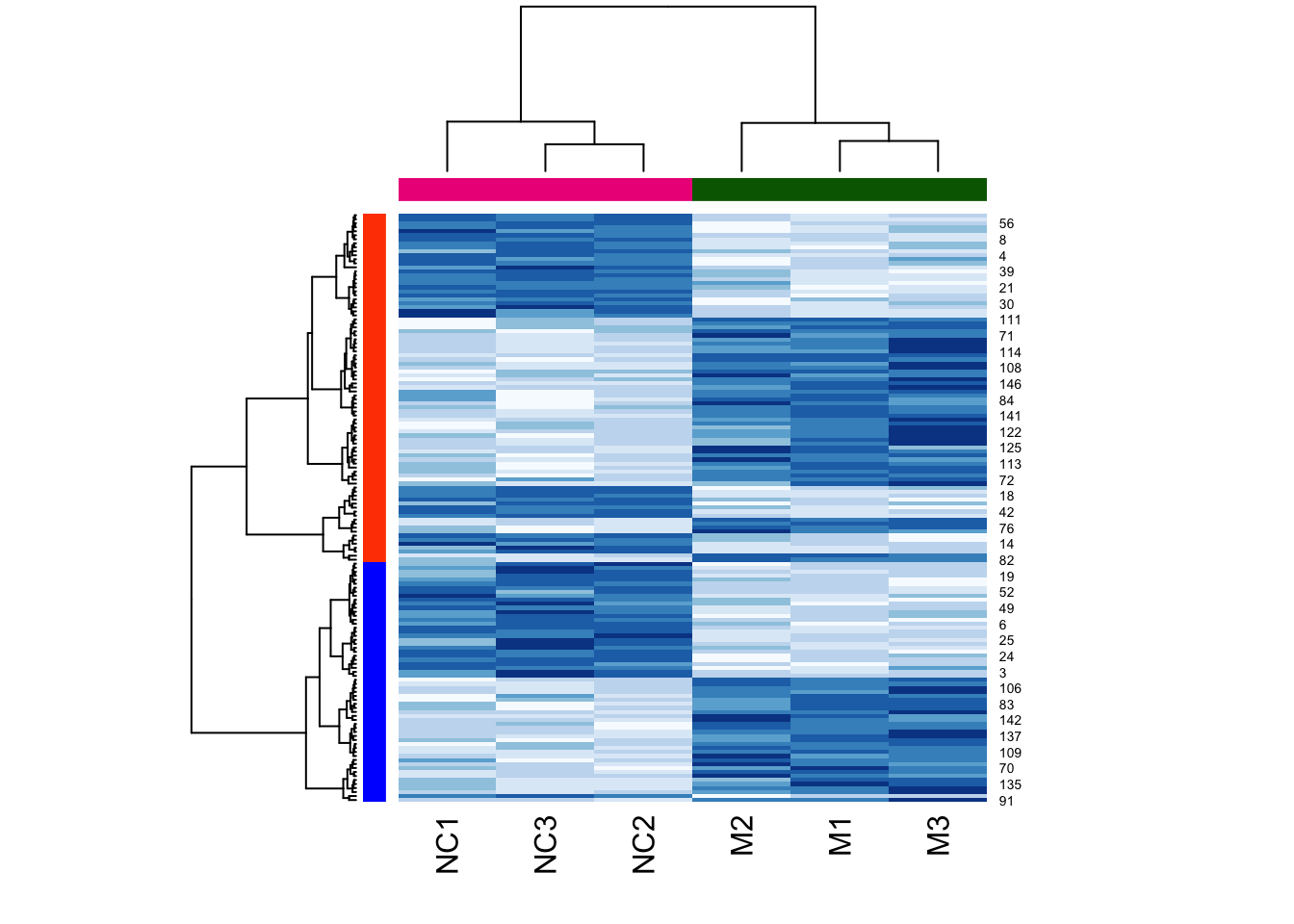
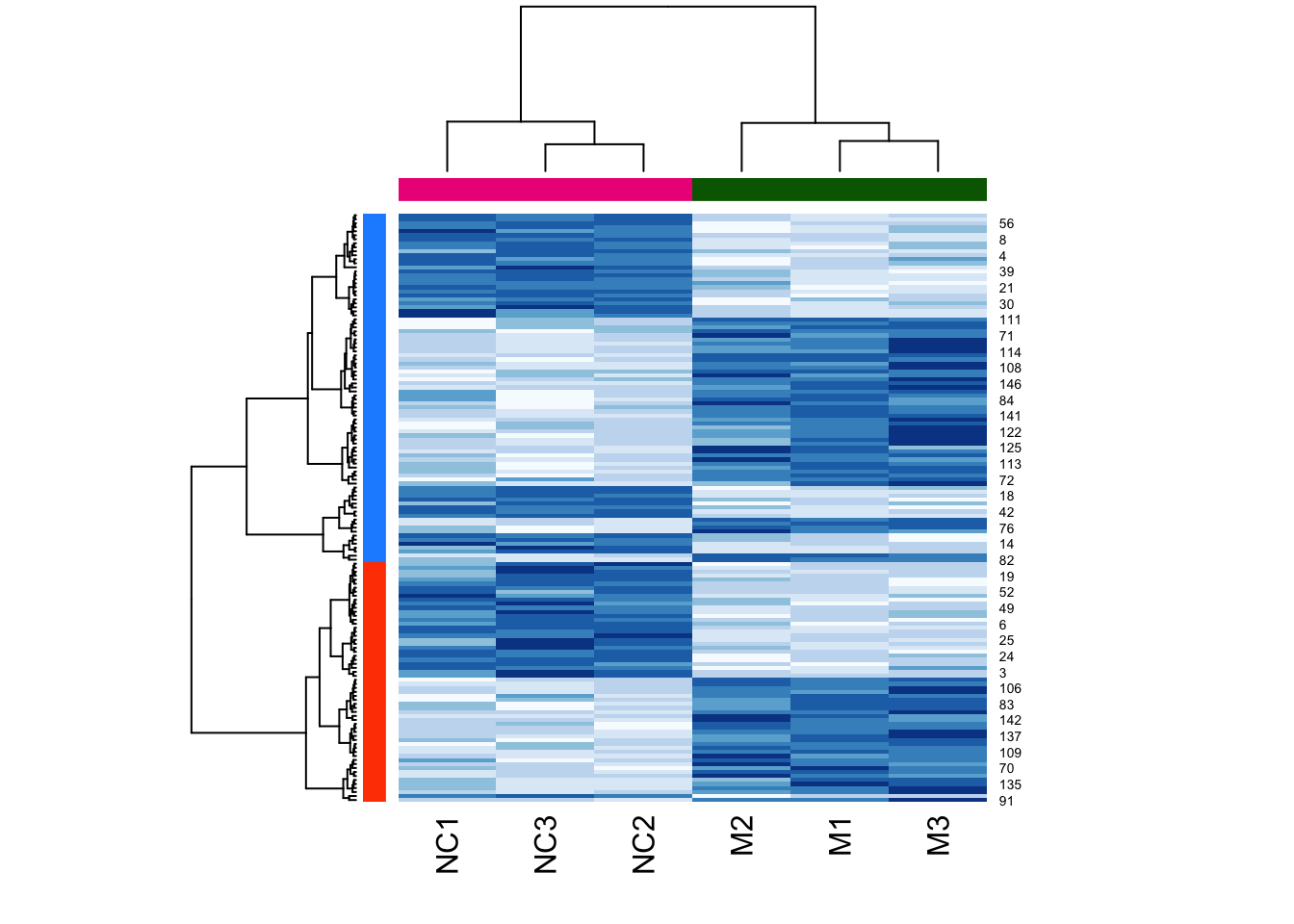
Note that the two colours are completely divided (i.e., there is no interspersed red and blue). This is a good sign that the clustering function used the identical clustering method, here, ward.D2, to cluster the samples.
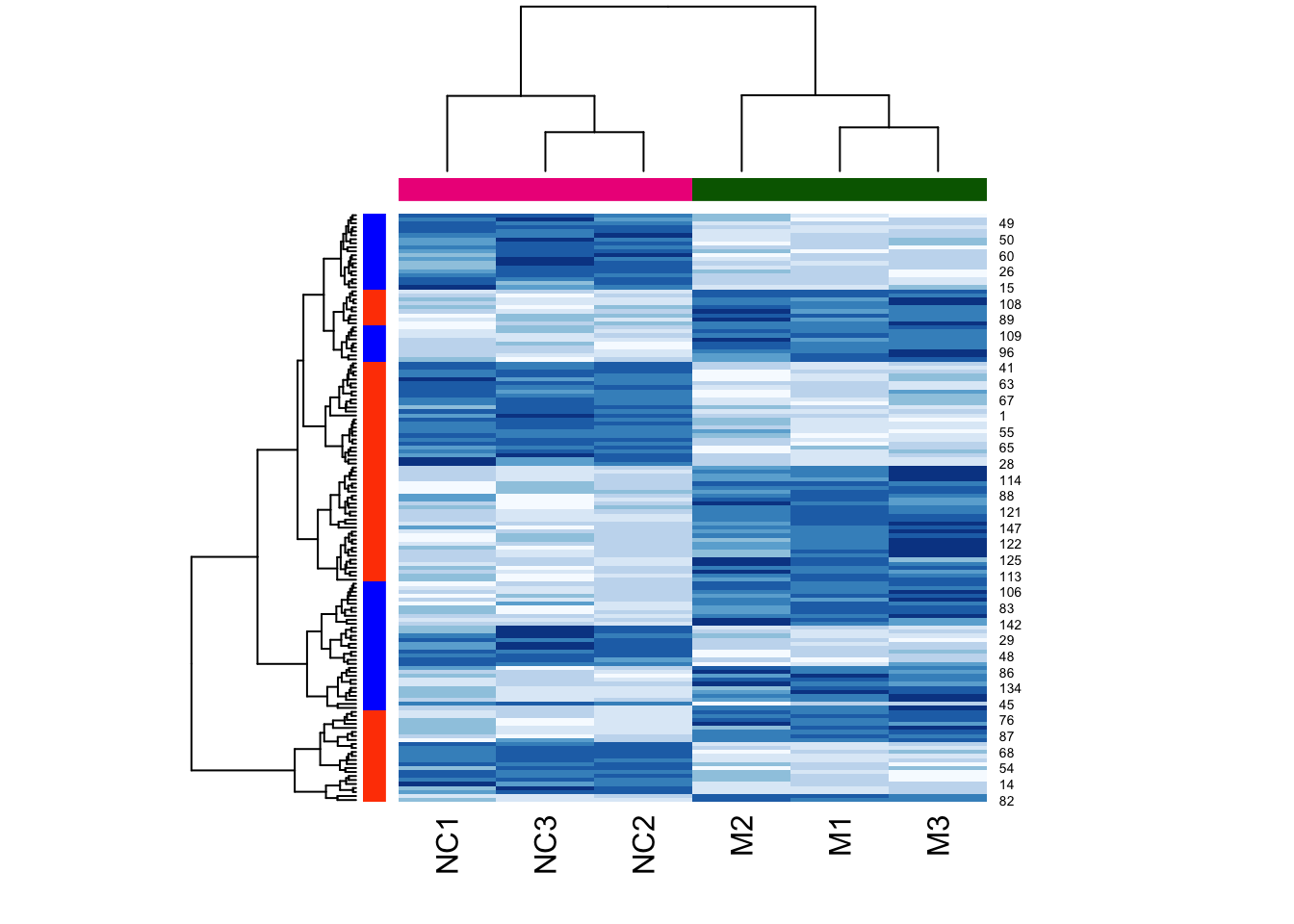
Compare this result to what happens if we try the same function call without clustering:
heatmap(
as.matrix(mouse_exp),
col = brewer.pal("Blues",n=8),
RowSideColors = h2cols, # use colours from cutree call above
ColSideColors = c(
rep("darkgreen",3),
rep("deeppink2",3)
)
)
K-means clustering
Let’s try using k-means clustering, asking for three clusters:
kclust <- kmeans(
mouse_exp,
centers = 3
)
kclust## K-means clustering with 3 clusters of sizes 64, 22, 61
##
## Cluster means:
## M1 M2 M3 NC1 NC2 NC3
## 1 5.553148 5.499583 5.642404 5.426931 5.435363 5.353342
## 2 7.416536 7.406216 7.414799 7.548674 7.534414 7.520608
## 3 3.947440 3.946048 4.012209 3.922949 3.950984 4.004362
##
## Clustering vector:
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## 1 3 3 1 1 3 1 1 1 3 2 3 1 2 3 1 2 2 3 1
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## 1 1 3 3 3 3 2 1 3 1 1 2 3 1 1 3 3 3 1 3
## 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
## 1 2 2 3 3 2 3 3 3 3 1 3 2 2 1 1 3 3 1 3
## 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
## 3 2 1 3 1 3 1 2 1 3 1 1 1 1 1 2 3 3 1 2
## 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
## 1 2 3 1 1 3 2 1 3 1 3 3 3 3 3 3 3 1 3 1
## 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120
## 3 1 3 3 3 3 2 1 3 1 1 3 1 1 1 1 2 2 3 1
## 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140
## 1 1 2 3 1 1 1 3 1 1 1 1 1 3 3 3 3 3 3 1
## 141 142 143 144 145 146 147
## 1 3 1 2 1 1 1
##
## Within cluster sum of squares by cluster:
## [1] 166.24343 81.44264 193.59229
## (between_SS / total_SS = 74.3 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss" "tot.withinss"
## [6] "betweenss" "size" "iter" "ifault"Using clValid to determine number of clusters
Use the clValid() function to validate clusters using the:
- Dunn index,
- silhouette scores, and
- connectivity
validation_data <- clValid(
mouse_exp,
2:6, # num. clusters to evaluate
clMethods = c("hier","kmeans"), # methods to eval.
validation = "internal"
)Let’s look at the results:
summary(validation_data)##
## Clustering Methods:
## hierarchical kmeans
##
## Cluster sizes:
## 2 3 4 5 6
##
## Validation Measures:
## 2 3 4 5 6
##
## hierarchical Connectivity 5.3270 14.2528 20.7520 27.0726 30.6194
## Dunn 0.1291 0.0788 0.0857 0.0899 0.0899
## Silhouette 0.5133 0.4195 0.3700 0.3343 0.3233
## kmeans Connectivity 13.2548 17.6651 37.3980 43.2655 50.6095
## Dunn 0.0464 0.0873 0.0777 0.0815 0.0703
## Silhouette 0.4571 0.4182 0.3615 0.3367 0.3207
##
## Optimal Scores:
##
## Score Method Clusters
## Connectivity 5.3270 hierarchical 2
## Dunn 0.1291 hierarchical 2
## Silhouette 0.5133 hierarchical 2All measures of clustering consistently indicate that two clusters best fit the data.
Now let’s cluster:
d <- dist(log(mouse_exp))
h <- hclust(d,method="ward.D2")
cluster_ids <- cutree(h, k = 2)
clust_colors <- c("dodgerblue","orangered")[cluster_ids]
heatmap(
as.matrix(mouse_exp),
col = brewer.pal("Blues",n=8),
hclustfun = hclust_fun,
RowSideColors = clust_colors, # kmeans labels
ColSideColors = c(
rep("darkgreen",3),
rep("deeppink2",3)
)
)
Exercise
For your exercise, try the following:
- Load the MASS package using:
library(MASS) - Import
crabsdataset using:data(crabs) - Learn about this dataset using:
?crabs - Extract the numeric columns describing the crab measurements (“FL”, “RW”, “CL”, “CW”, “BD”)
- Cluster the numeric columns using your method of choice
- Plot and color your data by clusters, by species (
sp), andsex - Do your clusters seem to separate these groups in the same way?